Eine systematische Annäherung an starke Passwörter.
Vorgeplänkel und Ausgangssituation
Passwörter sind allgegenwärtig. Wir benutzen sie um uns bei nahezu jedem Dienst im Internet oder am lokalen Rechner anzumelden – sei es für den Zugriff auf den E-Mail-Account, bei der Nutzung von Online-Shops oder Online-Banking, bei Foren, Newsgroups und sozialen Medien, bei Online-Spielen oder am lokalen Betriebssystem. Doch viele Untersuchungen haben gezeigt, dass die Verwendung von Passwörtern eigentlich dem widerspricht, wofür das menschliche Gehirn ausgelegt ist: wir können uns Bilder, Szenen und Erlebnisse gut merken, zufällige Zeichen- und Ziffernfolgen dagegen üblicherweise eher schlecht. Warum verwenden wir also diese Methode der Authentifizierung?
Ganz einfach: weil wir nichts besseres haben! Alle anderen Ansätze für Methoden, wie sich Menschen gegenüber Maschinen ausweisen können, besitzen ebenfalls gravierende Nachteile; die Details möchte ich an dieser Stelle nicht ausbreiten. Doch spielt es eine Rolle, was die ideale Art wäre, sich gegenüber einem Dienst zu authentifzieren? Nein, da die Realität aktuell – und bestimmt auch noch eine ganze Weile – auf Passwörter setzt. Wir müssen also das beste daraus machen.
Doch, was ist das beste? Der erfolgreiche Angriff auf iCloud-Passwörter prominenter Damen vor einigen Monaten hat gezeigt, dass hier immer wieder fatale Fehler passieren. Zur Erklärung: Die iCloud-Accounts, aus denen private Fotos gestohlen wurden, wurden geknackt, indem eine Vielzahl an möglichen Passwörtern ausprobiert wurde. Dabei kann man entweder auf typische Wörter-/Zeichenkombinationen, wie sie häufig als Kennwörter genutzt werden, setzen („Wörterbuch-Angriff“ bzw. „Dictionary-Attack“) oder man probiert stupide von „a“ bis „z“ alle möglichen Kombinationen durch („Brute-Force-Attack“). Offenbar hatten die betroffenen Personen keine starken Passwörter gewählt…
Starke Passwörter haben üblicherweise zwei zentrale Eigenschaften: sie sind lang und sie bestehen aus komplexen Kombinationen. Um einmal konsistente Aussagen über die Effektivität von Passwortlängen und -kombinationen treffen zu können, ziehe ich ein einfaches und plausibles Angriffsszenario heran: Der Angreifer ist in den Besitz des mit einem Hashwert gesicherten Passworts gelangt und möchte nun herausfinden, wie das Kennwort im Klartext heißt.
Ein Hashwert ist die bevorzugte Art, eine Passwort zu speichern: es wird mit einer Mathematischen Funktion (der Hashfunktion) in eine Bitfolge (den Hashwert) gewandelt. Diese Funktion hat zwei besondere Eigenschaften: sie kann nicht zurückgerechnet werden und sie liefert bei Eingabe des gleichen Passworts immer das gleiche Ergebnis. Möchte man also prüfen, ob ein Benutzer ein (vorher als Hashwert gespeichertes) Passwort korrekt eingegeben hat, so berechnet man den Hashwert der Eingabe und vergleicht ihn mit dem gespeicherten, denn ein Rückrechnen vom Hashwert auf das ursprüngliche Passwort ist nicht möglich. Da gleiche Passwörter immer die gleichen Hashwerte ergeben, muss bei korrekter Eingabe das Ergebnis das gleiche sein. Diese Methode wird übrigens verwendet, damit ein Administrator, der Zugriff auf die Benutzer-Datenbank hat, die Passwörter nicht sehen kann und damit noch ein gewisser Schutz besteht, wenn ein Angreifer an die Datenbankinhalte gelangen sollte.
Ich greife für mein Szenario auf die Ergebnisse eines Experiments zurück: Mit einer Kombination aus einer Reihe von Grafikkarten wurde ein Rechner gebaut, der bei erträglichen Kosten extrem schnell Passworthashes berechnen kann. Die Ergebnisse sind in der folgenden Abbildunge zusammengefasst; ich werde auf die Kalkulationsperformance von SHA1-Hashwerten zurückgreifen, da diese stärker als die (leider immer noch) häufig eingesetzen MD5-Hashes sind und somit eher einen Worst-Case (aus Angreifersicht) der heutigen Praxis darstellen.
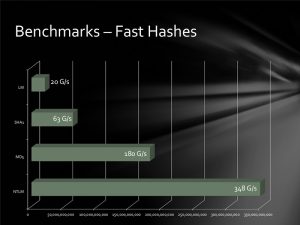
Die 63 Gigahashes/Sekunde bedeuten, dass es dem Rechner möglich war, 63 Milliarden SHA1-Hashes pro Sekunde zu berechnen. Dies wird meine Ausgangsbasis.
Passwörter und ihre Stärken
Viele Menschen neigen dazu, Passwörter nach einem sehr einfachen Schema zu bilden: <Wort>+<Zahl>. Das Wort ist häufig etwas aus dem eigenen Umfeld: der (Kose-)Name des Partners, eines Haustiers, Schauspielers oder Filmhelden, das eigene Auto, ein bestimmter Ort oder ein anderer Begriff, den man sich aus irgendeinem Grund leicht merken kann. An diesen wird dann – es wird ja üblicherweise die Verwendung von Ziffern durch eine Passwort-Policy durchgesetzt – einfach eine Zahl angehängt: die aktuelle Jahreszahl, Geburts- oder Hochzeitsdaten oder andere ebenfalls leicht merkbare Ziffernkombinationen. Was ist davon zu halten?
Die deutsche Sprache hat laut Duden etwa 500.000 Wörter. Vervierfacht man die Zahl, um noch Sonderformen und Umbildungen ebenso zu berücksichtigen wie Eigen- und Kosenamen sowie Slang-Ausdrücke, so landet man bei 2 Millionen unterschiedlichen Wörtern. Diese Zahl multipliziere ich mit einer weiteren Million, damit auch alle gängigen angehängten (und vorgestellten) Zahlenkombinationen großzügig einbezogen sind und erhalte eine Wert von 2 Billionen (2.000.000.000.000). Diese gefühlt große Anzahl an Passwörtern kann von der oben beschriebenen Maschine (65 Mrd. Hashes pro Sekunde) in nicht mehr als 31 Sekunden komplett durchprobiert werden!
Wenn diese Form von Passwörtern keinen wirklichen Schutz bietet, müssen Passwörter also anders aussehen. Verbreitet sich ein neues Passwort-Schema (wie beispielsweise das von XKCD vorgeschlagene), so wird auch dieses innerhalb kürzester Zeit von Passwort-Crackern berücksichtigt und ist damit ebenfalls verbrannt. Das einzige, das wirklich dauerhaft schützt, ist ein komplett zufällig erzeugtes Passwort. Doch auch hier gibt es viele Entscheidungen zu treffen: Wie lang muss es sein? Wie kompliziert (also aus wie vielen unterschiedlichen Zeichen bestehend) soll es sein?
Diesem Thema kann man sich seriös nur mit etwas Mathematik (genaugenommen: Kombinatorik) nähern. Zuerst definiere ich mir meinen Zeichenraum. So bezeichnet man die Menge der Zeichen, aus denen man das Passwort zufällig zusammenbaut. Ich berücksichtige dabei die folgenden Klassen:
- Kleinbuchstaben (26)
- Großbuchstaben (26)
- Ziffern (10)
- Sonderzeichen (26)
Ich nehme der Einfachheit halber 26 Sonderzeichen an, damit sie ebenso wie die Groß- und Kleinbuchstaben jeweils einen Zeichensatz aus 26 Buchstaben bilden.
Wie Berechnet man die Anzahl an möglichen Kombinationen für ein Passwort einer bestimmten Länge und aus einem bestimmten Zeichenvorrat?
- Besteht ein Passwort aus genau einer Ziffer (0-9), so gibt es genau 10 unterschiedliche Möglichkeiten (=10^1).
- Hat das Passwort zwei Ziffern, (00-99), so existieren 100 Möglichkeiten (=10^2).
- Besitzt ein Passwort der Länge 1 nur Kleinbuchstaben (a-z), so gibt es 26 unterschiedliche Kombinationen (=26^1).
- Bei zwei Kleinbuchstaben (aa-zz) gib es 676 (=26^2) Möglichkeiten.
Allgemein gesprochen ergibt sich folgende Formel: <Anzahl mögliche Zeichen>^<Länge des Passworts>. Ein Passwort, das aus 8 Zeichen (Kleinbuchstaben und Ziffern) besteht, besitzt also 2.821.109.907.456 (=(26+10)^8) Kombinationsmöglichkeiten.
Ich habe mich hingesetzt und eine Worst-Case-Analyse einer Brute-Force-Attacke auf übliche Passwortlängen durchgeführt. Dabei habe ich einfach die Anzahl möglicher Kombinationen bei bestimmten Zeichenvorräten und Passwortlängen ausgerechnet und eine Angriffsgeschwindigkeit von den oben beschriebenen 63 Gigahashes pro Sekunde veranschlagt. Zu beachten ist, dass statistisch betrachtet ein solcher Angriff nach dem Durchprobieren der Hälfte der möglichen Passwortkombinationen gelingt – die von mir angegebene Zeit muss also für die Average-Case-Analyse halbiert werden. Dies ändert jedoch nichts an der Größenordnung des Ergebnisses: wenn es im Worst-Case nur Sekunden dauert, so trifft das auch auf den Average-Case zu; muss man im (für den Angreifer) schlimmsten Fall von einigen Jahren Rechenzeit ausgehen, so gilt dies auch im statistisch relevanteren Mittel. Die Ergebnisse sind in der folgenden Tabelle zusammengefasst.
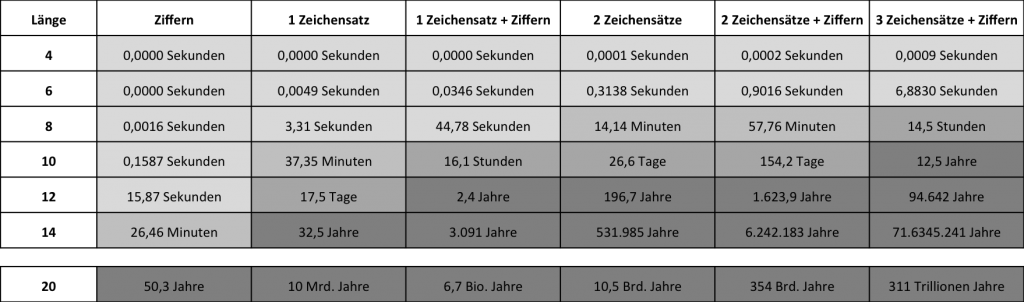
Das Alter des Universums beträgt übrigens ca. 14 Mrd. Jahre… 😉
Wenig überraschend zeigt sich bei dieser Betrachtung, dass längere Passwörter besser schützen als kürzere und dass auch die Hinzunahme von zusätzlichen Zeichensätzen unter Umständen eine deutliche Verbesserung bringt. Besonders interessant ist jedoch die folgende Überlegung: Ausgehend von einem Passwort aus 8 Zeichen (Klein- und Großbuchstaben sowie Ziffern), das in ca. einer Stunde geknackt werden kann; was ist die bessere Strategie – eine Erhöhung der Komplexität durch die Hinzunahme von Sonderzeichen oder die Verlängerung auf 10 Stellen? Die Antwort mag überraschen: Es ist signifikant besser, die Passwortlänge auf 10 Zeichen zu erhöhen (Dauer für Angriff: ca. 154,2 Tage) als Sonderzeichen hinzuzunehmen (Dauer für Angriff: ca. 14,5 Stunden)!
Der sinnvolle Umgang mit Passwörtern
Es zeigt sich also, dass Passwortlängen ein entscheidender Schlüssel zur Passwortsicherheit sind; Sonderzeichen sind gar nicht notwendig, wenn die Länge stimmt! Der Sicherheitsgewinn durch die Hinzunahme von Sonderzeichen wird sehr häufig überschätzt.
Wenn man nun ein gutes Passwort gewählt hat (also eines, das wirklich zufällig erzeugt wurde und nicht in einem Wörterbuch steht!), welche Gefahren drohen dann noch? Zuerst besteht die Gefahr, dass man das Passwort bei einem Dienst (z.B. einem Online-Shop) verwendet, dessen Anbieter damit nicht sorgsam umgeht. Es könnte unsicher gespeichert worden sein oder der Anbieter selbst (oder einer seiner Mitarbeiter) greift das Passwort ab, nachdem es gerade am Server angekommen ist. Verwendet man nun das gleiche Passwort noch an anderer Stelle, so wäre auch der dortige Account nun bedroht bzw. sogar geknackt – insbesondere, da als Benutzernamen häufig die immer gleichen E-Mail-Adressen zum Einsatz kommen.
Um diese gefährliche Wiederverwendung unbedingt zu vermeiden, empfehle ich die Verwendung eines Passwort-Safes (z.B. KeePass). Dabei handelt es sich um eine kleine Datenbank am eigenen Rechner (oder Smartphone), in dem die ganzen unterschiedlichen Passwörter verschlüsselt gespeichert werden. Nebenbei hat man üblicherweise auch gleich einen Zufallsgenerator, der einem Kennwörter für all die Dienste, die man so nutzt, erzeugt. Zugriff auf diese Passwörter erhält nur, wer ein Master-Passwort kennt, dass natürlich unbedingt sehr lang sein sollte! Einfach mal ein langes und zufälliges Passwort erzeugen und auswendig lernen. Wenn es einmal im Kopf drin ist, dann kann man es über einen sehr langen Zeitraum verwenden (wenn man es wirklich nur am Passwort-Safe eingibt)! Wie unsinnig ein häufiger Passwortwechsel ist, habe ich übrigens hier schon einmal beschrieben.
Hier also die sechs goldenen Regeln für den Umgang mit Passwörtern:
- Passwörter dürfen keine sinnvollen Wörter oder bedeutungsvolle Zahlen beinhalten. Auch der Einsatz von Leetspeak bietet übrigens keine Sicherheit und wird längst von Passwortcrackern berücksichtigt!
- Passwörter dürfen auf keinen Fall wiederverwendet werden. Für jeden Dienst muss ein separates Passwort erzeugt werden!
- Passwörter müssen lang sein. Das ist fast noch wichtiger als die Verwendung vieler unterschiedlicher Zeichensätze. Für ein Master-Passwort von Passwort-Safes empfehle ich mindestens 16 Stellen.
- Passwörter müssen eine gewisse Komplexität besitzen. Die Länge ist zwar wichtiger, aber zumindest Groß- und Kleinbuchstaben sollten es schon sein.
- Passwörter dürfen aufgeschrieben werden. Es spricht nichts dagegen, das Master-Passwort zur Sicherheit auf einen Zettel (niemals im Rechner!) aufzuschreiben. Natürlich muss diese Notiz sehr sorgsam verwahrt und sollte nicht im Geldbeutel herumgetragen werden.
- Passwörter müssen nicht ständig gewechselt werden. Wenn man mit seinem Master-Passwort sehr sorgfältig umgeht und es eine ausreichende Sicherheit bietet (Länge, Komplexität), dann kann man es gerne über Jahre nutzen – wer sollte es denn in „so kurzer Zeit“ herausfinden? 😉
